Why Learn Binary and What Is It?
Binary is a numeric system of only two values; 1 which signals ON, and 0 which signals OFF. We use these binary codes daily within our computers, whether they’re gigantic corporate and government processors, or simply our own laptops. All operate at their most basic level through binary; storing data, and running systems through zeros and ones.
Why learn binary? It’s the primary language of computers and files, allowing you to issue instructions, code and network. It’s also like learning a secret language – and what inner child doesn’t want that. The 0s and 1s translating into numbers, which in conjunction with ASCII, reveal a hidden world.
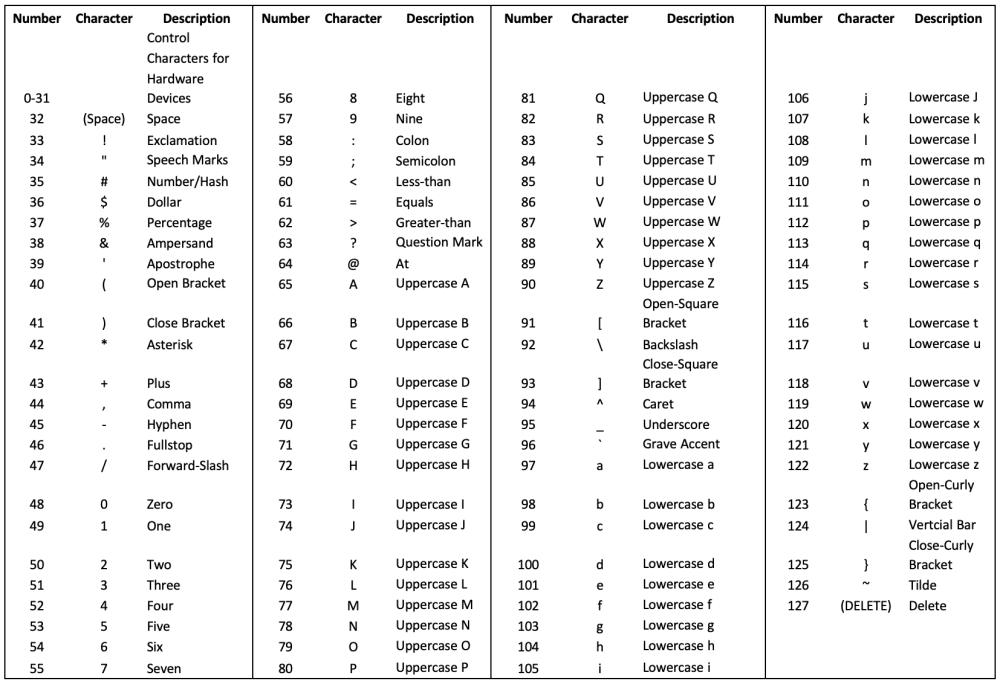
So what’s ASCII? This is the American Standard Code for Information Interchange, in which 128 English Characters (or instructions) are represented by a number from 0 to 127.
Writing and Understanding Binary
There’s only one rule to learning binary – don’t panic – it looks far scarier than it is. In fact, I’m far from a being a maths genius, still being unable to do my time tables, but once I took a deep breath and held a bar of chocolate (for consolation and consultation) I got it.
First thing, and you may already know it, is that there are only two decimal numbers within binary: 0 and 1.
The binary code 1 occurs when a number can’t be evenly divided by two, unless one is taken off – hence the code 1.
Let’s see this in an example: 23 can’t be evenly divided by 2, but take 1 off from 23, making it 22, and it becomes a number which can be evenly divided: 22/2=11. Therefore, the binary number is 1, as you had to take 1 off to make it an evenly divided number.
Let’s look at another example: 11, again this number can’t be evenly divided by 2, but take 1 off from 11, making it 10, and it can be evenly divided: 10/2=5. Making the binary number 1, as you had to take 1 off to make it evenly dividable.
The binary code 0 is given when no number is taken off for the number to divide evenly in two – hence the code 0.
The binary code 0 is given when the number can be evenly divided by 2. For example, 4 can be evenly divided by 2: 4/2=2, making the code 0 as no number was needed to be removed for it to evenly divide. In another example: 38/2=16, again no number is taken off for it to divide by 2, hence 0.
Producing a Binary Code
Now you understand why you get 1s and 0s, let’s work on producing a complete binary code. A complete binary code is when your number can no longer be divided downwards, as it’s reached the lowest denomination: zero. For example, say if you have the number 43, you keep dividing this downwards till you reach zero. Meanwhile every time you divided it, you would have a binary number of 1 or 0.
Let’s see this as an example:
43/2 can’t be evenly divided, so take off 1 (first binary number 1), making it 42/2=21
Then divide this remaining total: 21, but again 21 can’t be evenly divided by 2, so take off 1 (second binary number 1), making it 20/2=10.
As this remaining total of 10 can be evenly divided by 2, no number is taken off, making the binary number 0 (third binary number 0), with 10/2=5.
But again 5 can’t be evenly divided by 2, unless 1 is taken off (fourth binary number 1), making it 4/2=2.
Again 2 can be evenly divided, with no number being taken off (fifth binary number 0), 2/2=1.
But 1 can’t be divided, so you again take 1 off (sixth binary number 1), making it 0/2=0.
You therefore have the binary numbers 1, 1, 0, 1, 0, 1. However, when you write down the binary code for your number (43 in this case) you start the code off from the last number divided, which will always be one. Therefore, the binary code for 43 will in fact be written as 1, 0, 1, 0, 1, 1.
It’s easier to see this in a table format:

Remember you write the binary code from the lowest number upwards. So, for 43 the binary is written as 101011
Let’s look at another example, say we want to write down 23 in binary. First take this number and divide by 2, working your way down:
(Always divide by two, and don’t forget if it can’t divide evenly, take 1 off)

BUT remember the clincher, you write the binary code from the lowest number upwards. So, for 23 the binary is written as 10111
Let’s try another, calculating the binary code for the number 40:
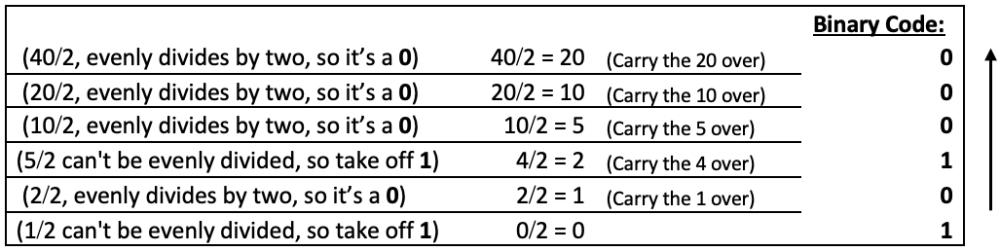
The binary code for 40 being written as 101000
Last example, but this time with no guide.
Creating the binary code for 93:
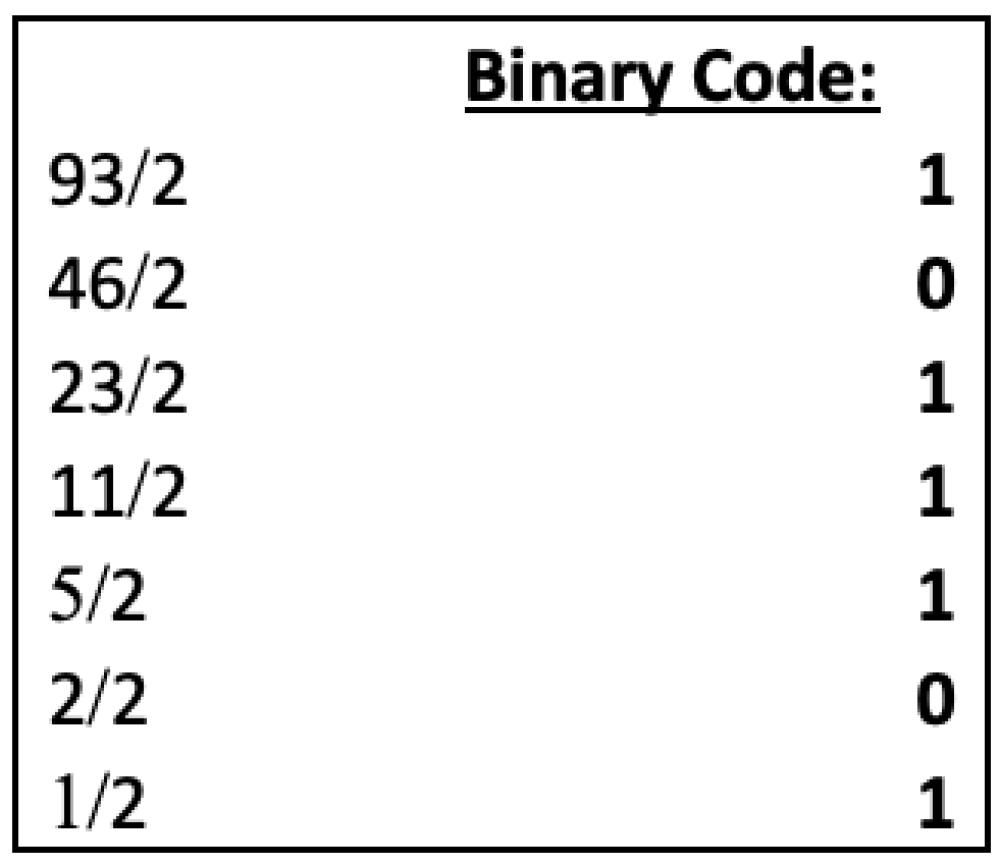
The binary being written as 1011101
Having Converted a Number to Binary, Let’s Now Do the Reverse and Convert Binary to a Number.
Now in understanding binary it follows the simple guideline of starting from 1 and always being to the power of two, in other words a multiplication of two (x2);

The (x2) list going on exponentially, or at least till you give up and decide to snack down with popcorn and Netflix instead.
It might seem strange to start the numbers from right to left but this is because binary is always written this way.
Confused? Yep! but it won’t last, for there’s a cheat you can use in understanding binary;
Simply write out a binary table going no higher than 128 (as the ASCII table only goes up to a decimal number of 127). The table should look like this:

Now say you have a binary code of 110111, simply write each 1 or 0 below each number, making sure to end at the number 1. It will look like this:

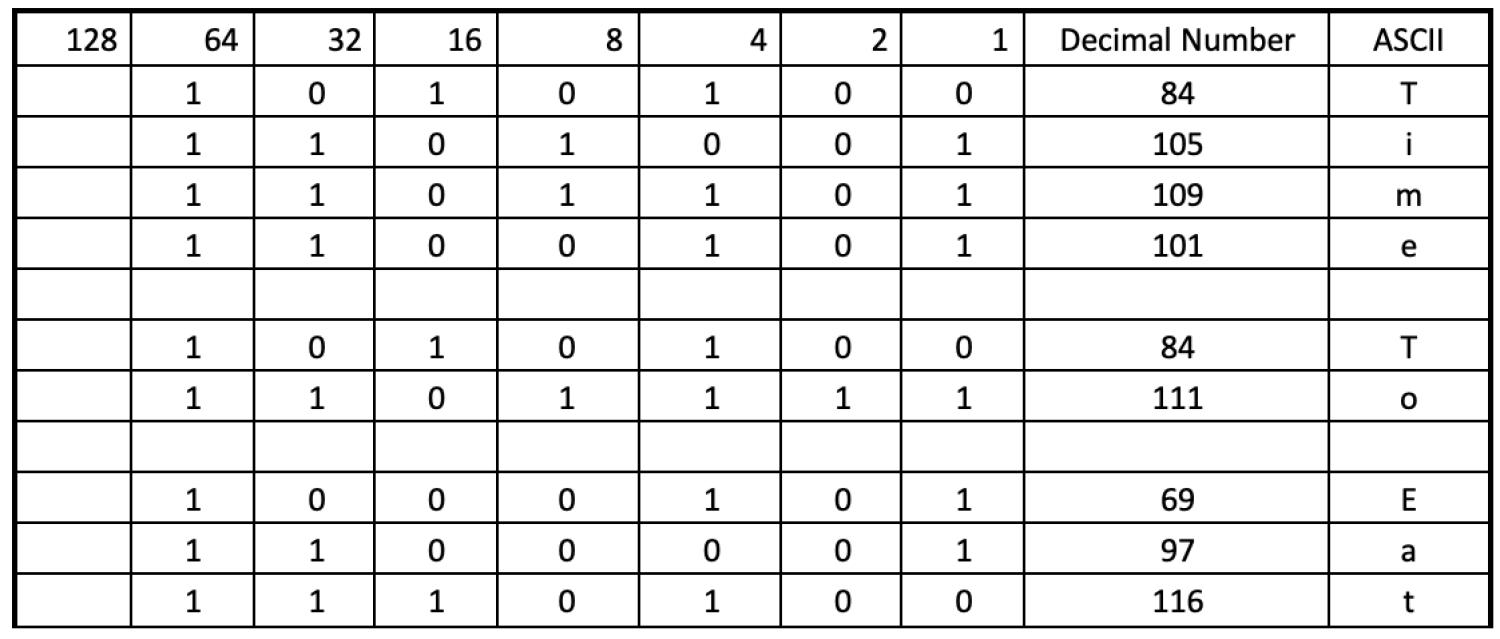
Next, only add together the numbers where a one is present e.g. 32 + 16 + 4 + 2 + 1 = 55. So the binary 110111 in decimal numbers is 55. Ta dah you have your answer.
In another example, let’s use a number we’ve already converted to binary (101000) and now convert it back to its number (40).

Again, make sure the binary code ends at 1, and only add the numbers where a 1 is present: 32 + 8 = 40.
Hopefully, you’re now comfortable in writing and understanding binary. Next, using this in conjunction with ASCII, let’s see how we can translate binary into the written English word.
Complete, all done!! Yay you now know binary inside and out, but as a little passing challenge, here is some binary to convert to numbers:
1000011 1101111 1100100 1100101
1000001 1110111 1100001 1111001
ASCII Table (ASCII Frequent Characters):